20.3 Helping Patients
We would like to close this chapter – and indeed the whole book - with an inspiring application of insights derived from the theory of neuronal dynamics to animals and, potentially, humans. Initial results at the current state of research are encouraging, so that mathematical considerations could ultimately increase the quality of life of, among others, Parkinsonian patients.
Parkinson is a severe brain disease. A prominent symptom in human patients suffering from Parkinson’s disease is involuntary shaking of arms and fingers in a periodic movement of about 3-6 Hz, called resting tremor. Some patients also exhibit muscle rigidity or akinesia where they are unable to move. Tremor as well as rigidity are correlated with overly strong oscillatory synchronization in brain areas such as thalamus and basal ganglia, whose activity in the healthy state is asynchronous ( 387; 366; 504 ) . Moreover, the oscillation frequency of neural activity is related to the tremor frequency.
| A | B |
|---|---|
|
|
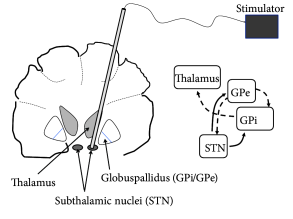
One of the presently available treatments of Parkinsonian symptoms is ‘Deep Brain Stimulation’ (DBS) ( 47; 46 ) . DBS reduces both tremor and rigidity of Parkinsonian patients. To perform DBS, a high-frequency stimulus is applied to an electrode implanted in the sub-thalamic nucleus or globus pallidus (which project indirectly or directly onto the thalamus) of the patient (Fig. 20.11 A). The treatment is reversible so that, when stimulation is stopped, patients rapidly fall back into tremor or rigidity.
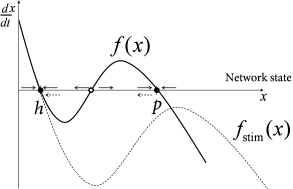
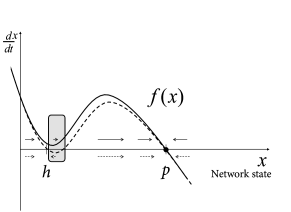
If we view the brain as a dynamical system, we can say that classical DBS shifts the state of the brain so as to reduce the symptoms of Parkinson during stimulation, but does not return the brain’s autonomous dynamics back to a healthy state. In other words, the patient relies on continuous treatment through DBS. We may visualize the pathological and healthy conditions as two different configuration in some abstract space of network states. It is reasonable to assume that brain dynamics in the healthy state is at a stable equilibrium point - despite ongoing spike firing and plasticity on different time scales; otherwise our brains would rapidly stop functioning. The fact that, after the end of DBS, the brain returns to the pathological state indicates that this state is also stable (Fig. 20.11 B).
The question arises whether, by suitable stimulation protocols, it would be possible to shift the pathological brain back into its healthy state. Work of the group of Peter Tass ( 506; 507 ) , but also other groups ( 449; 445; 551 ) suggests that this may be possible. The treatment relies on the idea that the pathological state of strong oscillations is probably linked to pathologically strong intra-network connections (Fig. 20.10 C). An ideal stimulation protocol should thus not only interfere with the oscillations but also lead to a rewiring of the network with weaker connections so that, even when the stimulus is removed, the network does not immediately fall back into the strong oscillatory mode.
| A | B |
|---|---|
|
|
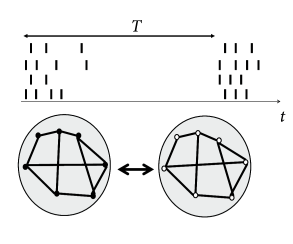
How can we interfere with an ongoing synchronized oscillation? As discussed in Section 20.2 , neurons in an oscillatory state can be described by a phase . An electric pulse delivered by an electrode tends to synchronize neurons in the neighborhood of the electrode by shifting their phases by an amount that depends on the current phase of the neuron. If several electrode fibers are used in the same network, local groups surrounding the tips of the fibers can be stimulated at different moments in time. Therefore, the phase within each group is reset by roughly the same amount, but the phase shift varies between groups. Consider a stimulation of four fibers given at a relative interval of (Fig. 20.12 ). With such a stimulation paradigm, the global network synchronization is perturbed by the ‘coordinated reset’ of the four subpopulations ( 506 ) . With eight or twenty independent electrode fibers one could spread out the stimulation (and therefore the phases of neuronal oscillators) even more equally over one period. However, the number four is a reasonable compromise and bundles of four fibers attached together so as to form one single electrode device are readily available.
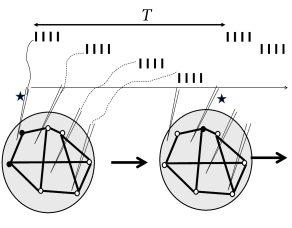
If a single sequence of four ‘coordinated reset’ pulses is given to four electrode fibers, the network returns, after some transient into the synchronized oscillation. In order to make the asynchronous state stable, the network wiring needs to be changed. Hebbian synaptic plasticity requires neurons to be active. It is therefore important to choose a stimulation protocol which suppresses synchronous oscillations, but not neuronal activity per se . The ‘coordinated reset’ fulfills this condition since it does not silence the neural oscillators but just shifts their phases. Therefore, if the ’coordinated reset’ stimulation is repeated again and again, so as to keep network activity in a state of asynchronous firing for a sufficiently long time, we may expect that synaptic plasticity causes a rewiring of the network connectivity. Once the network is rewired, the stimulus can be removed.
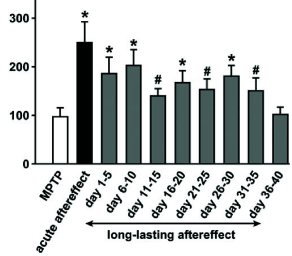
Indeed, when monkeys suffering from Parkinsonian symptoms have received a few hours of DBS with the ‘coordinated reset’ protocol, symptoms are reduced and remain at a reduced level for more than 24 hours (Fig. 20.13 B), before they slowly drift back into the oscillatory state ( 507 ) . The beneficial effects of ‘coordinated reset’ stimulation therefore last at least 10 times longer than those of traditional DBS where tremor reappears rapidly.
From the perspective of dynamical systems, these results suggest that the healthy state of Parkinsonian patients is not globally stable. However, since the ‘ruins’ (cf. Ch. 4 ) of the fixed point corresponding to healthy asynchronous activity persist, a shift of the network into the neighborhood of the healthy state leads to a slow down of the dynamics so that the network remains for a long time in the neighborhood of the healthy condition (Fig. 20.13 C).
Traditional protocols of DBS have been found by trial and error. The standard protocol consists of continuous high-frequency stimulation ( 100Hz) at rather large amplitude ( 47 ) . Remarkably, the mathematical perspective provided by the theory of dynamical systems together with intensive computational modeling ( 506; 449; 551; 395 ) has now led to protocols that work with reduced amplitude and do not require continuous stimulation. Instead, only a few hours of stimulation per day promise to suffice ( 507 ) . Eventually, we may hope that these or related ( 445 ) protocols will be translated from monkeys to humans and increase the quality of life of patients suffering from severe forms of Parkinson’s disease. Interestingly, the ’coordinated reset’ protocol has already found a first successful application in humans suffering from Tinnitus ( 505 ) .
| A | B |
|---|---|
|
|