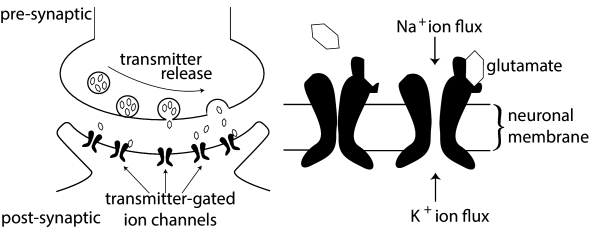
3 Dendrites and Synapses 3 Dendrites and Synapses 3.2 Spatial Structure: The Dendritic Tree

3.1 Synapses

In the previous chapter, we have encountered two classes of ion channels, namely voltage-activated and calcium-activated ion channels. The third type of ion channel we have to deal with are the transmitter-activated ion channels involved in synaptic transmission (see Fig. 3.1) and generally activated from outside the cell. Activation of a presynaptic neuron results in a release of neurotransmitters into the synaptic cleft. The transmitter molecules diffuse to the other side of the cleft and activate receptors that are located in the postsynaptic membrane. So-called ionotropic receptors have a direct influence on the state of an associated ion channel. Metabotropic receptors control the state of an ion channel by means of a biochemical cascade of G proteins and second-messengers. In both cases, the activation of the receptor results in the opening of certain ion channels and, thus, in an excitatory or inhibitory postsynaptic transmembrane current (EPSC or IPSC).

Instead of developing a mathematical model of the transmitter concentration in the synaptic cleft, we keep things simple and describe transmitter-activated ion channels as an explicitly time-dependent conductivity $g_{\text{syn}}(t)$ that will open whenever a presynaptic spike arrives. The current that passes through a synaptic channel depends, as before, on the difference between its reversal potential $E_{\text{syn}}$ and the actual value of the membrane potential,

I_{\text{syn}}(t)=g_{\text{syn}}(t)\,(u(t)-E_{\text{syn}})\,.

(3.1)

The parameter $E_{\text{syn}}$ and the function $g_{\text{syn}}(t)$ can be used to describe different types of synapses. For inhibitory synapses $E_{\text{syn}}$ is usually set to $-75$ mV, whereas for excitatory synapses $E_{\text{syn}}\approx 0$ .

Typically, a superposition of exponentials is used for $g_{\text{syn}}(t)$ . A simple choice for the time course of the synaptic conductance in Eq. 3.1 is an exponential decay

g_{\text{syn}}(t)=\sum_{f}\bar{g}_{\text{syn}}\,{\text{e}}^{-(t-t^{(f)})/\tau}% \,\Theta(t-t^{(f)})\,,

(3.2)

with a time constant of, e.g., $\tau=5$ ms and an amplitude of $\bar{g}_{\text{syn}}=40$ pS. Here, $t^{(f)}$ denotes the arrival time of a presynaptic action potential and $\Theta(x)$ is the Heaviside step function.

For some synapse types, a single exponential decay is not sufficient. Rather, the postsynaptic current is made up of two different components, a fast one with a decay time constant of a few milliseconds, and a second one that is often ten times slower. If we also take into account the smooth rise of the synaptic response, the postsynaptic conductance is of the form

g_{\text{syn}}(t)=\sum_{f}\bar{g}_{\rm syn}\,[1-{\text{e}}^{-(t-t^{(f)})/\tau_% {\text{rise}}}]\,\left[a\,{\text{e}}^{-(t-t^{(f)})/\tau_{\text{fast}}}+(1-a)\,% {\text{e}}^{-(t-t^{(f)})/\tau_{\text{slow}}}\right]\Theta(t-t^{(f)})\,,

(3.3)

where $a$ is the relative weight of the fast component. The time constant $\tau_{\text{rise}}$ characterizes the rise time of the synaptic conductance.

Example: A more detailed synapse model

Instead of considering a synapse with a fixed time course $g_{\text{syn}}(t)\,$ , we can also make a model which has the flavor of a Hodgkin-Huxley channel. We describe the synaptic conductance $g_{\text{syn}}(t)=g_{\rm max}\,R(t)$ , by its maximal conductance $g_{\rm max}$ and a gating variable $R$ , where $R(t)$ is the fraction of open synaptic channels. Channels open when neurotransmitter $N$ binds to the synapse

{dR\over dt}=\alpha\,N\,(1-R)-\beta\,R,

(3.4)

where $\alpha$ is the binding constant, $\beta$ the unbinding constant and $(1-R)$ the fraction of closed channels where binding of neurotransmitter can occur. Neurotransmitter $N$ is released with each presynaptic spike so that the total amount of neurotransmitter at synapse $j$ is

N(t)=\int_{0}^{\infty}\gamma(s)\,S_{j}(t-s)\,ds,

(3.5)

where $S_{j}=\sum_{f}\delta(t-t_{j}^{(f)})$ is the presynaptic spike train (a sequence of $\delta$ -functions, see Chapter 1) and $\gamma(s)$ is the time course of the neurotransmitter density as measured at the site of the postsynaptic receptor. More advanced synaptic signaling schemes can be designed along the same line of argument (125)

Fig. 3.1: A. Schema of synaptic transmission. Upon arrival of a presynaptic spike, neurotransmitter spills into the synaptic cleft and is captured by postsynaptic receptors. B. Schema of a postsynaptic AMPA receptor of an excitatory synapse. When glutamate is bound to the receptor, sodium and potassium ions can flow through the membrane.

3.1.1 Inhibitory Synapses

The effect of fast inhibitory neurons in the central nervous system of higher vertebrates is almost exclusively conveyed by a neurotransmitter called $\gamma$ -aminobutyric acid, or GABA for short. A characteristic feature of inhibitory synapses is that the reversal potential $E_{\text{syn}}$ is in the range of -70 to -75 mV. Thus, if the neuronal membrane potential is above the reversal potential, presynaptic spike arrival leads to a hyperpolarization of the neuron, making action poential generation less likely. However, the same presynaptic spike would lead to a depolarization of the membrane if the neuron has its membrane potential at -80 mV or below.

There are many different types of inhibitory interneurons (329; 263). Biologists distinguish between two major types of inhibitory synapse, called GABA ${}_{\rm A}$ and GABA ${}_{\rm B}$ . Both synapse types use GABA as the neurotransmitter. GABA ${}_{\rm A}$ channels are ionotropic and open exclusively for chloride ions, whereas GABA ${}_{\rm B}$ synapses have metabotropic receptors that trigger a comparatively slow signaling chain ultimately leading to the opening of $K^{+}$ channels. Consequently the value of the synaptic reversal potential $E_{\text{syn}}$ depends for GABA ${}_{\rm A}$ synapses on the concentration of chloride ions inside and outside the cell, while that of GABA ${}_{B}$ synapses depends on the potassium concentrations.

Example: GABA ${}_{\rm A}$ synapse model

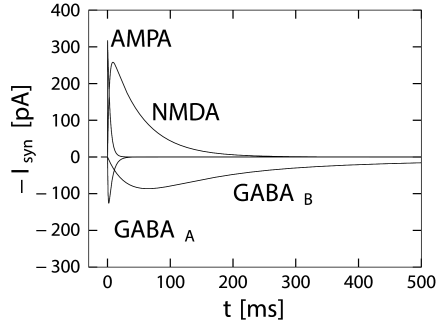
GABA ${}_{\rm A}$ synapses have a fast time course that can be approximated by a single term in Eq. (3.3) with $a=1$ , $\tau_{\rm rise}\approx$ 1 ms, and a time constant $\tau_{\rm fast}\approx$ 6 ms (Destexhe and Pare (127); Fig. 3.2) which has also been deemed 3 times larger. More complex models are sometimes used (125).

Example: GABA ${}_{\rm B}$ synapse model

This is a slow inhibitory synapse working via a second-messanger chain. Common models use Eq. (3.3) with a rise time of about 25-50ms, a fast decay time in the range of 100-300ms and a slow decay time of 500-1000ms. The fast component accounts for about 80 percent of the amplitude of conductance ( $a=0.8$ ) (125; 334), illustrated in Fig. 3.2.

3.1.2 Excitatory Synapses

Most excitatory synapses in the vertebrate central nervous system rely on glutamate as their neurotransmitter. The postsynaptic receptors, however, can have very different pharmacological properties and different types of glutamate receptor units can be present in a single synapse. These receptors are classified using artificial drugs such as NMDA or AMPA that act as selective agonists. NMDA (N-methyl-D-aspartate) binds to channels with NMDA receptors, but not to other glutamate receptors. The most prominent among those glutamate receptors that do not respond to NMDA are the AMPA-receptors³³AMPA is short for $\alpha$ -amino-3-hydroxy-5-methyl-4-isoxalone propionic acid.. AMPA is an artificial glutamate. Channels with AMPA-sensitive receptors are called ‘AMPA channels’ because these channels react to AMPA, whereas channels with NMDA-sensitive receptors do not open upon application of AMPA. However, both NMDA and AMPA channels react to the natural form of glutamate that the nervous system uses as neurotransmitter.

AMPA receptors consist of four subunits, each with a glutamate binding site. Most AMPA receptors contain the subunit called GluR2. If an AMPA-receptor channel containing GluR2 is open, sodium and potassium ions can pass, but calcium ions can not. Synaptic channels with AMPA-receptors are characterized by a fast response to presynaptic spikes and a quickly decaying postsynaptic current.

NMDA-receptor controlled channels are significantly slower and have additional interesting properties that are due to a voltage-dependent block by magnesium ions (220). In addition to sodium and potassium ions, also calcium ions can pass through open NMDA-channels.

Fig. 3.2: Dynamics of post-synaptic current (3.1) after a single pre-synaptic spike at $t=0$ . GABA ${}_{\rm A}$ , GABA ${}_{\rm B}$ , AMPA, and NMDA without magnesium block are shown for a post-synaptic neuron at rest ( $u=-65$ ).

Example: Conductance of glutamate channels with AMPA-receptors

The time course of the postsynaptic conductivity caused by an activation of AMPA-receptors at time $t=t^{(f)}$ is sometimes described by Eq. (3.2) with a decay time of about 2-5ms (166; 125).

Example: Conductance of glutamate channels with NMDA-receptors

NMDA-receptor controlled channels exhibit a rich repertoire of dynamic behavior because their state is not only controlled by the presence or absence of glutamate, but also by the membrane potential. At resting potential, the NMDA channel is blocked by a common extracellular ion, Mg ${}^{2+}$ (220), even if glutamate is present. If the membrane is depolarized beyond $-50$ mV, the Mg ${}^{2+}$ -block is removed, the channel opens when glutamate binds to the receptor and, thereafter, stays open for 10 – 100 milliseconds. A simple model of the voltage dependence of NMDA-receptor controlled channels is

g_{\text{NMDA}}(t)=\bar{g}_{\text{NMDA}}\cdot\left[1-{\text{e}}^{-(t-t^{(f)})/% \tau_{\text{rise}}}\right]\,{\text{e}}^{-(t-t^{(f)})/\tau_{\text{decay}}}\,g_{% \infty}(u,[\text{Mg}^{2+}]_{\text{o}})\,\Theta(t-t^{(f)})\,,\inner@par\text{% with }g_{\infty}(u,[\text{Mg}^{2+}]_{\text{o}})=\left(1+\beta\,{\text{e}}^{% -\alpha\,u}\,[\text{Mg}^{2+}]_{\text{o}}\right)^{-1}\,,

(3.6)

with $\tau_{\text{rise}}$ in the range of 3 ms to 15 ms, $\tau_{\text{decay}}$ in the range of 40 ms to 100 ms, $\bar{g}_{\text{NMDA}}=1.5$ nS, $\alpha=0.062\,\text{mV}^{-1}$ , $\beta=1/(3.57~{}{\rm mM})$ , and an extracellular magnesium concentration $[\text{Mg}^{2+}]_{\text{o}}=1.2$ mM (334; 166).

What is the potential functional role of NMDA receptors? First, their comparatively long time constant keeps a trace of presynaptic events and acts as a low-pass filter. Second, even though NMDA-receptor controlled ion channels are permeable to sodium and potassium ions, their permeability to Ca ${}^{2+}$ is five or ten times larger. Calcium ions are known to play an important role in intracellular signalling and are probably involved in long-term modifications of synaptic efficacy. Calcium influx through NMDA-controlled ion channels can occur if presynaptic spike arrival (leading to glutamate release from presynaptic sites) coincides with a depolarization of the postsynaptic membrane (leading to removal of the Mg ${}^{2+}$ -block). Hence, NMDA-receptors operate as molecular coincidence detectors between pre- and postsynaptic events.

3.1.3 Rapid synaptic dynamics

Parameters of a synaptic contact point are not fixed, but can change as a function of the stimulation history. Some of these changes are long-lasting and are thought to represent the neuronal correlate of learning and memory formation. The description of these learning-related changes will be treated in Chapter 19. Here we concentrate on dynamic changes of the synapse that do not persist but decay back to their normal values within hundreds of milliseconds or a few seconds. These changes are called short-term synaptic plasticity.

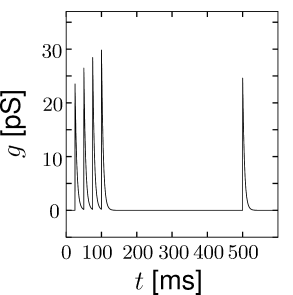
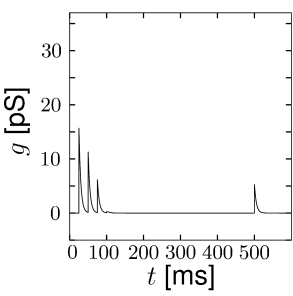
Short-term synaptic plasticity can be measured if a presynaptic neuron is stimulated so as to generate a sequence of spikes. Synaptic facilitation means that the apparent amplitude of a postsynaptic current in response to the second spike is larger than that to the first spike. Synaptic depression is the opposite effect (Figure 3.3).

Fig. 3.3: Short-term plasticity. A synapse is activated by 4 presynaptic spikes and a fifth spike 400 ms later. A. At a facilitating synapse, the effect of the second and third spike is larger than that of the first spike. The effect of a spike after a pause of 400 millisecond is approximately that of the first spike (time constant $\tau_{P}=200ms$ ). B. At a depressing synapse, successive spikes in a periodic spike train have less and less effect. $400$ ms later, the synapse has partially recovered, but is still significantly depressed ( $\tau_{P}=500ms$ ).

As a simple model of synaptic facilitation and depression (112), we assume that the maximal synaptic conductance $\bar{g}_{\rm syn}$ in Eq. (3.2) or (3.3) depends on the fraction $P_{\rm rel}$ of presynaptic sites releasing neurotransmitter. Facilitation and depression can both be modeled as presynaptic processes that modify $P_{\rm rel}$ . With each presynaptic spike, the number of available presynaptic release sites changes. Between spikes the value of $P_{\rm rel}$ returns exponentially to its resting value $P_{0}$ . Thus,

{dP_{\rm rel}\over dt}=-{{P_{\rm rel}-P_{0}}\over\tau_{P}}+f_{F}\,(1-P_{\rm rel% })\,\sum_{f}\delta(t-t^{f})

(3.7)

where $\tau_{P}$ is a time constant, $f_{F}$ controls the degree of facilitation, and $t^{f}$ denotes the times of presynaptic spike arrivals.

The model of a depressing synapse is completely analogous. The amount of neurotransmitter available for release develops according to the differential equation

{dP_{\rm rel}\over dt}=-{{P_{\rm rel}-P_{0}}\over\tau_{P}}-f_{D}\,P_{\rm rel}% \,\sum_{f}\delta(t-t^{f})

(3.8)

where $\tau_{P}$ is a time constant and the parameter $f_{D}$ with $0<f_{D}<1$ controls the amount of depression per spike.

The total effect of presynaptic spikes depends on the available neurotransmitter as well as the value $g_{0}$ of postsynaptic conductance if all synaptic ion channels are open, so that, for depressing or facilitating synapses, we can use Eq. (3.2) with a value $\bar{g}_{\rm syn}=P_{\rm rel}\,g_{0}$ . This procedure has been used to generate Fig. 3.3.