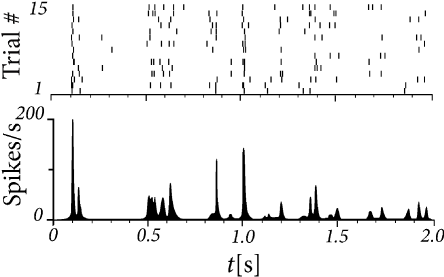
Many in vivo experiments show noisy behavior of cortical neurons. The activity of neurons from the visual cortex, for example, can be recorded while a slowly moving bar is presented on a screen within the visual field of the animal. As soon as the bar enters the neuron’s receptive field the firing rate goes up. The spike train, however, varies considerably from trial to trial, if the same experiment is repeated several times. Similarly, neurons in a region of the sensory cortex of rats or mice respond systematically to whisker movements, but the response is somewhat different between one trial and the next. Furthermore, the very same neuron occasionally emits a spontaneous spike, even if no external stimulus is applied. During spontaneous activity, the voltage trajectory fluctuates considerably and intervals between one spike and the next exhibit a large degree of variability (Fig. 7.1).

Are these experiments convincing evidence for ubiquitous noise in the central nervous system? The above observations refer to experiments on the neural system as a whole. The cortical neuron that is recorded from, does not only receive input from the sensors, but also from many other neurons in the brain. The effective input to this neuron is basically unknown. It is thus possible that there is a substantial fluctuation in the input current to cortical neurons, even though the external (e.g., visual or tactile) stimulus is always the same.

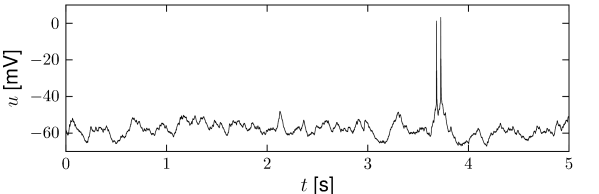
The advantage of experiments in vitro is that the stimulus injected into the neuron can be well controlled. If the stimulation consists of a known time-dependent current directly injected into the neuron, the neuronal response also varies from one trial to the next, even if the very same stimulation is repeated several times (Fig. 7.2). Is this an indication of ‘real’ noise? The variability is visible only if the stimulating current is nearly constant (Fig. 7.3). In fact, when neurons are driven by a current with large-amplitude fluctuations of the input signal, neurons behave more or less deterministically (80; 324).

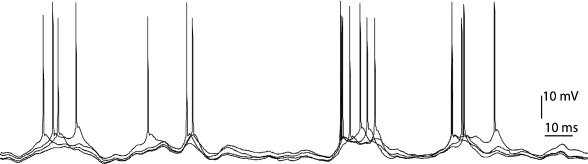
Similarly, in the full and intact brain, neurons react much more reliably to a rapidly changing external stimulus than to constant or slowly moving stimuli. For example, spatially uniform random flicker of an image elicits more or less the same spike train in retinal ganglion cells if the same flicker sequence is presented again (51). A similar behavior has been reported for motion-sensitive neurons of the visual system in flies (115) and monkey cortex (37); see Fig. 7.4 for an example of a cortical neuron. Whether a neuron behaves nearly deterministically or rather randomly thus depends, at least to a certain extent, on the stimulus.

In the following, we distinguish between intrinsic noise sources that generate stochastic behavior on the level of the neuronal dynamics and are present even in an isolated neuron in vitro; and extrinsic sources that arise from network effects and synaptic transmission naturally occurring in vivo.

A source of noise, which is literally omnipresent, is thermal noise. Due to the discrete nature of electric charge carriers, the voltage $u$ across any electrical resistor $R$ fluctuates at finite temperature (Johnson noise). The variance of the fluctuations at rest is $\langle\Delta u^{2}\rangle\propto R\,k\,T\,B$ where $k$ is the Boltzmann constant, $T$ the temperature and $B$ the bandwidth of the system. Since neuronal dynamics is described by an equivalent electrical circuit containing resistors (cf. Chapter 2), the neuronal membrane potential fluctuates as well. Fluctuations due to Johnson noise are, however, of minor importance compared to other noise sources in neurons (327).

Another source of noise that is specific to neuronal cells and present already in an isolated neuron arises from the finite number of ion channels in a patch of neuronal membrane. Most ion channels have only two states: they are either open or closed. The electrical conductivity of a patch of membrane for ion type $i$ is proportional to the number of open ion channels. For a given constant membrane potential $u$, a fraction $P_{i}(u)$ of ion channel of type $i$ is open on average. The actual number of open channels fluctuates around $N_{i}\,P_{i}(u)$ where $N_{i}$ is the total number of ion channels of type $i$ in that patch of membrane; see Fig. 2.5 in Chapter 2.

The formulation of the Hodgkin-Huxley equations in terms of ion channel conductivities (see Chapter 2) is implicitly based on the assumption of a large number of ion channels so that fluctuations can be neglected. Since, in reality, $N_{i}$ is finite, the conductivity fluctuates and so does the potential. If the membrane potential is close to the threshold, channel noise can be critical for the generation of action potentials. Models that take the finite number of ion channels into account, can reproduce the observed variability of real neurons with intracellular stimulation (456; 96). In particular, they show little spike jitter if the input current is rapidly changing, but are less reliable if the input current is constant.

Apart from intrinsic noise sources at the level of an individual neuron there are also sources of noise that are due to signal transmission and network effects (extrinsic noise). Synaptic transmission failures, for instance, seem to impose a substantial limitation to signal transmission within a neuronal network. Experiments with double electrode recordings from two synaptically connected neurons suggest that only 10–30 percent of presynaptic spikes generate a postsynaptic response (218; 330).

Finally, an important part of the irregularity of neuronal spiking during spontaneous activity seems to be due to properties of the network – even if the network itself is completely deterministic. Model studies show that networks of excitatory and inhibitory neurons with fixed random connectivity can produce highly irregular spike trains – even in the absence of any source of noise. An example of variability in a deterministic network of leaky integrate-and-fire neurons with random excitatory and inhibitory interactions is shown in Fig. 7.5. We will discuss the underlying mechanisms in Part III of this book (see Sections 12.3.4 and LABEL:section-irregular-oscillations). As a result of the network activity, each neuron receives as input an irregular spike sequence that can be described as stochastic spike arrival; cf. Chapter 8. The difference between the large variability of neurons in vivo compared to the variability during intracellular stimulation in vitro can therefore be, at least partially, attributed to network effects.