Chapter 12 Neuronal Populations

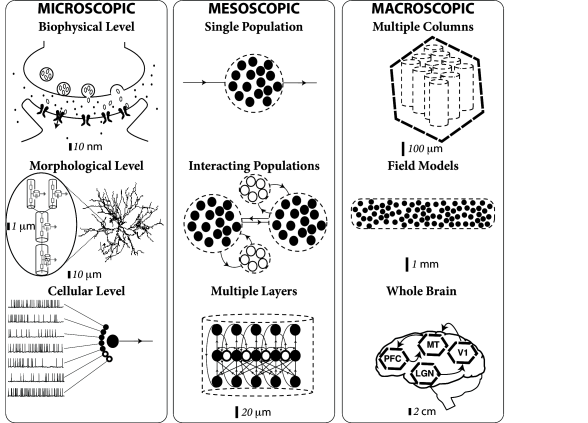
The brain contains millions of neurons which are organized in different brain areas, within a brain area in different subregions, inside each small region into different layers, inside each layer into various cell types. The first two parts of this book focused on the mathematical description of an isolated neuron. Starting with this chapter, we shift our attention to the collective properties of groups of neurons, which we call ‘neuronal populations’. Instead of modeling the spike times of a single neuron which belongs, e.g., to the cell class ‘Pyramidal’ in Layer 5 of subregion C4 in brain region S1 (the numbers here are completely arbitrary), we can ask the question: Suppose a human subject or animal receives a visual, auditory, or somatosensory stimulus – what is the activity of all the cells in this layer of this subregion that are of type ‘pyramidal’ in response to the stimulus? What is the response of this subregion as a whole? What is the response of a brain area? In other words, at any of the scales of spatial resolution (Fig. 12.1), we may be interested in the response of the neuronal population as a whole, rather than in the spikes of individual neurons.

The general idea is presented in Fig. 12.2. A network of 10 000 neurons consisting of $N_{E}$=8 000 excitatory and $N_{I}$=2 000 inhibitory neurons, has been simulated while the excitatory neurons received a time-dependent input. Instead of analyzing the spike trains of one or two neurons, we count the number of spikes in a small time step (say $\Delta t=$ 1ms) across all the excitatory neurons in the network. After dividing by $\Delta t$ and $N_{E}$, we arrive at the population activity $A(t)$ of the group of excitatory neurons; cf. Section 7.2 in Chapter 7. Analogously, we can determine the population activity of the inhibitory neurons or that of the network as a whole. The central questions of this and the following chapters is: Can we predict the population activity $A(t)$ from the properties of its neurons and the network connectivity? How does the population activity respond to a novel input?

The aim of this chapter is to provide the foundation of the notions of ‘neuronal population’ and ‘population activity’. In the first section we argue that the organization of cortex into columns and layers provides the biological substrate of ‘neuronal populations’. In Section 12.2 we identify the mathematical assumptions and idealizations that will enable us to predict the population activity from single-neuron properties. The basic idea is that, for the definition of a neuronal population, we should group neurons with similar properties together. The aim of Sections 12.2 and 12.3 is to make this intuition more precise. In Section 12.4 we give a first example of the population activity approach by analyzing stationary activity in a highly connected population. The notions developed in this chapter will be used in the next two chapters in order to analyze the dynamics of one or several connected populations.