Part II Generalized Integrate-and-Fire Neurons

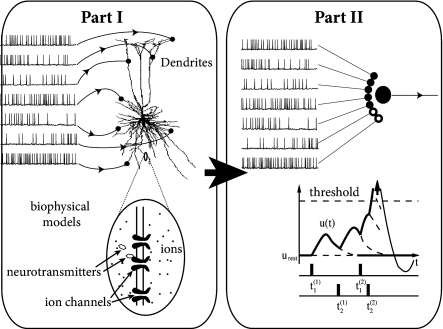
In Part II we exploit the mathematical and biophysical foundations that were layed in Part I in order to reduce the complexity of neuron models. Part II is focused on simplified phenomenological models in which spikes are generated by a threshold criterion, possibly in combination with a stochastic process. We start in Ch. 5 with a determinstic one-dimensional integrate-and-fire model. It turns out that such a model is not powerful enough to account for firing properties of real neurons so that we add adaptation variables to (Ch. 6) and stochasticity (Chs. 7 – 9). These simplified neuron models, often called generalized integrate-and-fire models or generalized linear models, can be systematically fitted to experimental data (Ch. 10). Moreover they allow a transparent discussion of neuronal encoding in (and decoding of) stochastic spike trains (Ch. 11). The simplified neuron models of part II will be the starting point of the analysis of large neuronal networks in part III.