7 Variability of Spike Trains and Neural Codes
Neuronal Dynamics

7.3 Interval distribution and coefficient of variation

The estimation of interspike interval (ISI) distributions from experimental data is a common method to study neuronal variability given a certain stationary input. In a typical experiment, the spike train of a single neuron (e.g., a neuron in visual cortex) is recorded while driven by a constant stimulus. The stimulus might be an external input applied to the system (e.g., a visual contrast grating moving at constant speed); or it may be an intracellularly applied constant driving current. The spike train is analyzed and the distribution of intervals sks_{k} between two subsequent spikes is plotted in a histogram. For a sufficiently long spike train, the histogram provides a good estimate of the ISI distribution which we denote as P0⁢(s)P_{0}(s); cf. Fig. 7.9. The interval distribution can be interpreted as a conditional probability density

P0(s)=P(t(f)+s|t(f))P_{0}(s)=P(t^{(f)}+s|t^{(f)}) (7.12)

where ∫tt+Δ⁢tP(t′|t(f))dt′\int_{t}^{t+\Delta t}P(t^{\prime}|t^{(f)})\,{\text{d}}t^{\prime} is the probability that the next spike occurs in the interval [t,t+Δ⁢t][t,t+\Delta t] given that the last spike occurred at time t(f)t^{(f)}.

A B
Fig. 7.9: Stationary interval distribution. A. A neuron driven by a constant input produces spikes with variable intervals. B. A histogram of the interspike intervals s1,s2,…s_{1},s_{2},\dots can be used to estimate the interval distribution P0⁢(s)P_{0}(s).

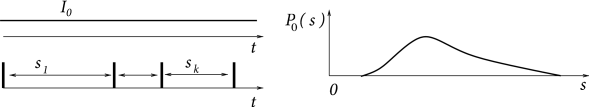In order to extract the mean firing rate from a stationary interval distribution P0⁢(s)P_{0}(s), we start with the definition of the mean interval,

⟨s⟩=∫0∞s⁢P0⁢(s)⁢d⁢s.\langle s\rangle=\int_{0}^{\infty}s\,P_{0}(s)\,{\text{d}}s\,. (7.13)

The mean firing rate is the inverse of the mean interval

ν=1⟨s⟩=[∫0∞s⁢P0⁢(s)⁢d⁢s]-1\nu={1\over\langle s\rangle}=\left[\int_{0}^{\infty}s\,P_{0}(s)\,{\text{d}}s\,% \right]^{-1} (7.14)

7.3.1 Coefficient of variation CVC_{V}

Interspike interval distributions P0⁢(s)P_{0}(s) derived from a spike train under stationary conditions can be broad or sharply peaked. To quantify the width of the interval distribution, neuroscientists often evaluate the coefficient of variation, short CVC_{V}, defined as the ratio of the standard deviation and the mean. Therefore the square of the CVC_{V} is

CV2=⟨Δ⁢s2⟩⟨s⟩2,C_{V}^{2}={\langle\Delta s^{2}\rangle\over\langle s\rangle^{2}}\,, (7.15)

where ⟨s⟩=∫0∞s⁢P0⁢(s)⁢d⁢s\langle s\rangle=\int_{0}^{\infty}sP_{0}(s)\,{\text{d}}s and ⟨Δ⁢s2⟩=∫0∞s2⁢P0⁢(s)⁢d⁢s-⟨s⟩2\langle\Delta s^{2}\rangle=\int_{0}^{\infty}s^{2}\,P_{0}(s)\,{\text{d}}s-% \langle s\rangle^{2}. A Poisson process produces distributions with CV=1C_{V}=1. A value of CV>1C_{V}>1, implies that a given spike train is less regular than a Poisson process with the same firing rate. If CV<1C_{V}<1, then the spike train is more regular. Most deterministic integrate-and-fire neurons fire periodically when driven by a constant stimulus and therefore have CV=0C_{V}=0. Intrinsically bursting neurons, however, can have CV>1C_{V}>1.

Example: Poisson process with absolute refractoriness

We study a Poisson neuron with absolute refractory period Δabs\Delta^{\rm abs}. For times since last spike larger than Δabs\Delta^{\rm abs}, the neuron is supposed to fire stochastically with rate rr. The interval distribution of a Poisson process with absolute refractoriness (Fig. 7.10A) is given by

P0⁢(s)={0fors<Δabsr⁢exp⁡[-r⁢(s-Δabs)]fors>Δabs;P_{0}(s)=\left\{\begin{array}[]{*{2}{c@{\qquad}}c}0\qquad&{\rm for}\qquad&s<% \Delta^{\rm abs}\\ r\,\exp\left[-r\,(s-\Delta^{\rm abs})\right]\qquad&{\rm for}\qquad&s>\Delta^{% \rm abs}\end{array}\right.\,; (7.16)

and has a mean ⟨s⟩=Δabs+1/r\langle s\rangle=\Delta^{\rm abs}+1/r and variance ⟨Δ⁢s2⟩=1/r2\langle\Delta s^{2}\rangle=1/r^{2}. The coefficient of variation is therefore

CV=1-Δabs⟨s⟩.C_{V}=1-{\Delta^{\rm abs}\over\langle s\rangle}\,. (7.17)

Let us compare the CVC_{V} of Eq. (7.17) with that of a homogeneous Poisson process of the same mean rate ν=⟨s⟩-1\nu=\langle s\rangle^{-1}. As we have seen, a Poisson process has CV=1C_{V}=1. A refractory period Δabs>0\Delta^{\rm abs}>0 lowers the CVC_{V}, because a neuron with absolute refractoriness fires more regularly than a Poisson neuron. If we increase Δabs\Delta^{\rm abs}, we must increase the instantaneous rate rr in order to keep the same mean rate ν\nu. In the limit of Δabs→⟨s⟩\Delta^{\rm abs}\to\langle s\rangle, the CVC_{V} approaches zero, since the only possible spike train is regular firing with period ⟨s⟩\langle s\rangle.

© Cambridge University Press. This book is in copyright. No reproduction of any part of it may take place without the written permission of Cambridge University Press.