16 Competing Populations and Decision Making 16.1 Perceptual Decision Making 16.3 Dynamics of decision making

16.2 Competition through common inhibition

The essential features of the experiments of Roitman and Shadlen (443) can be described by a simple model of decision making where neuronal populations compete with each other through shared inhibition.

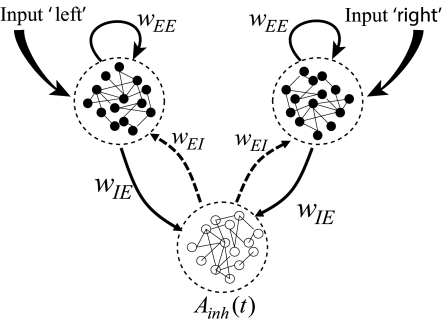
We consider a network of spiking neurons (Fig. 16.4) consisting of two excitatory populations interacting with a common pool in inhibitory neurons (543). Within the two excitatory populations neurons are randomly connected with connection weight $w_{EE}$ . Connections to and from the inhibitory populations have weights $w_{IE}$ and $w_{EI}$ , respectively. Neuronal parameters and connection weights are adjusted such that, in the absence of external input, all neurons exhibit spontaneous activity at low firing rates. In other words, the network is in a state of asynchronous irregular firing.

Fig. 16.4: Competition between neuronal pools. Two populations of excitatory neurons interact with a common pool of inhibitory neurons. Input signals indicating movement to the left are fed into population 1 with activity $A_{E,1}(t)$ . Each population of excitatory neurons makes excitatory connections of strength $w_{EE}$ onto itself. The inhibitory population receives input of strength $w_{IE}$ from the two excitatory populations and sends back inhibition of strength $w_{EI}$ .

Fig. 16.5: Competition between neuronal pools. A. Top: Spiking activity of two populations in trial 1 (left) and trial 2 (right). Dots denote spikes. Average across the population gives the population activities $A_{E,1}(t)$ and $A_{E,2}(t)$ . During presentation of an unbiased stimulus (e.g., equal number of points moving to the left and to the right), one of the excitatory population develops a high population activity, while the other one is suppressed, indicating a spontaneous decision to the left (trial 1) or to the right (trial 2). Bottom: An unbiased stimulus corresponds to an input to the left and right population of equal mean, but different realizations of noise. B. The dynamics of population activities $A_{E,1}(t),A_{E,2}(t)$ can be visualized in the phase plane. In the absence of stimulation, the activity of both excitatory populations exhibits a low firing rate of less than 5Hz (circle). Upon stimulation, the dynamics converge either to the region corresponding to ‘decision left’ (characterized by high values of $A_{E,1}$ ) or to ‘decision right’ (characterized by high values of $A_{E,2}$ ); adapted from (543).

Stimulation corresponds to a positive mean input into one or both groups of excitatory neurons. For example, for a description of the experiments of Roitman and Shadlen discussed in the previous section, we can identify input into population 1 as indicating coherent motion of the random dot pattern to the left whereas input into population 2 indicates motion to the right (Fig. 16.4). Since the stimulus in the experiments has a random component (e.g., the fraction of coherent dots is less than 100 percent), the input into each population is described as a mean plus some noise.

If the pattern has a high degree of coherence and moves to the left, the mean input to population 1 is high. This induces a high activity $A_{E,1}$ which in turn excites the inhibitory population which transmits inhibition to both excitatory pools. However, only the stimulated pool can overcome the inhibition so that the activity of the other excitatory population is suppressed. Since, at most one of the two populations can be active at the same time, the two populations are said to ‘compete’ with each other. The competition is induced by the shared inhibition. If the external stimulus favors one of the two populations, the population receiving the stronger stimulus ’wins’ the competition. In the absence of external stimulation, or for a weak unbiased stimulus, both populations exhibit low activity.

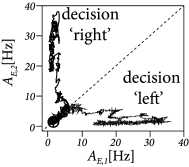
To highlight the dynamics of competition, let us now focus on a strong, but unbiased stimulus. Here, unbiased means that, after stimulus onset, both excitatory populations receive an input of the same mean, but with a different realization of the noise (Fig. 16.5A). Immediately after the onset of stimulation, both excitatory populations increase their firing rates. Soon afterward, however, one of the activities grows further at the expense of the other one, which is suppressed. The population which develops a high activity is called the ‘winner’ of the competition. In the next section, we will show mathematically how the shared inhibition induces a competition between the two excitatory populations.