19 Synaptic Plasticity and Learning
Neuronal Dynamics

19.4 Reward-based learning

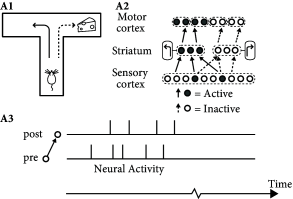
In conditioning experiments, animals learn complex action sequences if the desired behavior is rewarded. For example, in a simple T-maze an animal has to decide at the bifurcation point whether to turn left or right (Fig. 19.14 A). In each of several trials, the same arm of the maze is baited with a piece of cheese that is hidden in a hole in the floor and therefore neither visible nor smellable. After a few trials the animal has learned to reliably turn into the baited arm of the maze.

Unsupervised Hebbian learning is of limited use for behavioral learning, because it makes no distinction between actions that do and those that do not lead to a successful outcome. The momentary sensory state at the bifurcation point is represented by activity in the sensory cortices and, possibly, in hippocampal place cells. The action plan ‘turn left’ is represented by groups of cells in several brain areas likely to include striatum, whereas the final control of muscle activity involves areas in motor cortex. Therefore, during the realization of the action plan ‘turn left’ several groups of neurons are jointly active (Fig. 19.14 A). Unsupervised Hebbian learning strengthens the connections between the jointly active cells so that, at the next trial, it becomes more likely that the animal takes the same decision again. However, turning left does not lead to success if the cheese is hidden in the other branch of the maze.

A B
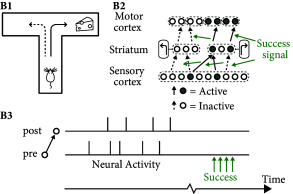
Fig. 19.14: Hebbian learning versus reward-modulated Hebbian learning in a T-maze decision task (schematic). The momentary sensory state of the animal is encoded by the layer of sensory cortex neurons; the action plan by a set of striatal neurons; and the motor output by neurons in motor cortex. A. Hebbian learning. Joint activity of neurons in sensory, striatal, and motor areas strengthens the links between the active neurons, despite the fact that turning left does not lead to success. B. Reward-modulated Hebbian learning. Joint activity of pre-and postsynaptic neurons strengthens connections only if, within a delay of a few seconds, a success signal is broadcast in the brain.

In order to solve the above task, two important aspects have to be taken into account that are neglected in unsupervised Hebbian learning rules. First, rules of synaptic plasticity have to take into account the success of an action. Neuromodulators such a dopamine are ideal candidates to broadcast a success signal in the brain (Fig. 19.15 ), where success can loosely be defined as ‘reward minus expected reward’ ( 460; 461; 462 ) . Second, the success often comes with a delay of a few seconds after an action has been taken; cf. Fig. 19.14 B. Thus, the brain needs to somehow store a short-term memory of past actions. A suitable location for such a memory are the synapses themselves.

Fig. 19.15: Dopamine encodes reward minus expected reward. A. The activity of dopaminergic neurons (PSTH) increases at the moment when a reward R occurs. B. If a conditioning stimulus such as a tone beep or a light reliably occurs one second before the reward, the same neurons no longer respond to the reward but after the CS that predicts the reward. C If the reward is predicted by the CS but not given, the PSTH exhibits a dip below the baseline (dashed lines) at the moment when the reward is expected. Schematic figure summarizing data from Schultz et al. (460).
A B
Fig. 19.16: Dopamine-modulated Hebbian learning. A. An STDP protocol normally gives rise to long-term potentiation (pre-before-post, solid black line as in Fig. 19.4D). However, if dopamine receptors are blocked, no change occurs (Schematic representation of experiments in Pawlak and Kerr (390)). B. The STDP window in a control situation (dashed line and filled data points) changes if additional extracellular dopamine is present (solid lines, large open squares); adapted from Zhang et al. (565).

The above two points can be used to formulate a first qualitative model of reward-modulated Hebbian learning. In Hebbian learning, weight changes Δ⁢wi⁢j\Delta w_{ij} depend on the spikes p⁢r⁢ejpre_{j} of the presynaptic neuron jj and the state p⁢o⁢s⁢tipost_{i} of the postsynaptic neuron ii . Correlations between the pre- and postsynaptic activity are picked up by the Hebbian function H⁢(p⁢r⁢ej,p⁢o⁢s⁢ti)H(pre_{j},post_{i}) . We assume that synapses keep track of correlations by updating a synaptic eligibility trace

τe⁢   d      d   ⁢t⁢ei⁢j=-ei⁢j+H⁢(p⁢r⁢ej,p⁢o⁢s⁢ti).\tau_{e}{{\text{d}}\over{\text{d}}t}e_{ij}=-e_{ij}+H(pre_{j},post_{i})\,. (19.46)

If the joint activity of pre- and postsynaptic neuron stops, the Hebbian term HH vanishes and the eligibility trace decays back to zero with a time constant τe\tau_{e} . The Hebbian term HH could be modeled by one of the rate models in the framework of Eq. ( 19.2.1 ) or an STDP model such as the one defined in Eq. 19.10 .

The update of synaptic weights requires a nonzero-eligibility trace as well as the presence of a neuromodulatory success signal MM

   d      d   ⁢t⁢wi⁢j=M⋅H⁢(p⁢r⁢ej,p⁢o⁢s⁢ti)⁢ei⁢j.{{\text{d}}\over{\text{d}}t}w_{ij}=M\cdot e_{ij}\,. (19.47)

While in standard Hebbian learning synaptic plasticity depends on two factors (i.e. pre- and postsynaptic activity), weight changes in Eq. ( 19.47 ) now depend on three factors, i.e., the two Hebbian factors and the neuromodulator MM . The class of plasticity rules encompassed by Eq. ( 19.47 ) is therefore called three-factor learning rules. In models of reward-based learning, the modulator signal MM is most often taken as ‘reward minus expected reward’

M⁢(t)=R⁢(t)-⟨R⟩,M(t)=R(t)-\langle R\rangle\,, (19.48)

where RR denotes the reward and the expectation ⟨R⟩\langle R\rangle is empirically estimated as a running average. The time constant τe\tau_{e} is typically chosen in the range of one second, so as to bridge the delay between action choice and final reward signal.

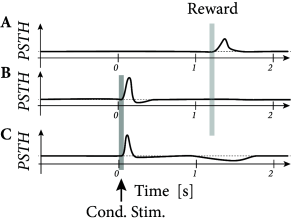
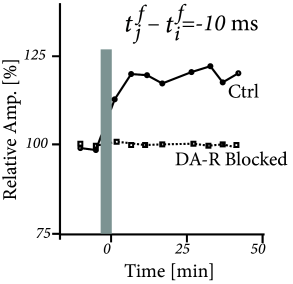
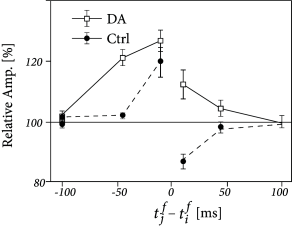
Three-factor rules have been suggested for rate-based ( 429; 307 ) as well as spike-based Hebbian models. In spike-based Hebbian models, the Hebbian term is often taken as a standard pair-based STDP function ( 238; 294; 153 ) or an STDP model that also depends on postsynaptic voltage ( 396; 153; 39 ) . Experiments have shown that the shape of the STDP window is indeed modulated by dopamine as well as other neuromodulators (Fig. 19.16 ); for a review see ( 391 ) .

Example: R-STDP and learning of spike sequences

Suppose a table tennis player plays a serve or a piano player a rapid scale. In both cases the executed movements are extremely rapid, have been practiced many times, and are often performed in ‘open loop’ mode, i.e., without visual feedback during the movement. There is, however, feedback after some delay which signals the success (or failure) of the performed action, e.g. the ball went off the table or the scale contained a wrong note.

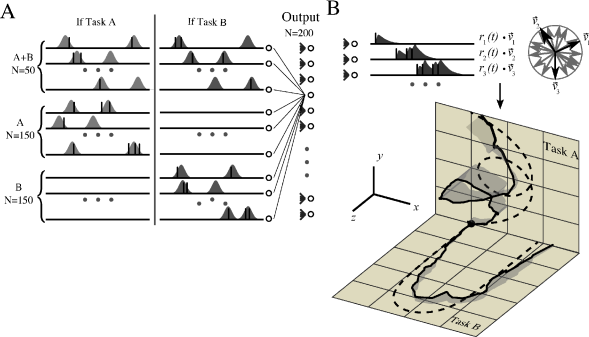
A rapid scale on a piano means touching about 10 different keys per second. Similarly, the complex gliding movement to give the ball its spin takes less than a second. It is likely that for such fast movements spike timing plays an important role. Motor cortex is involved in the control of limb movements. Experimental data from the arm area of primary motor cortex indicates that populations of neurons encode the direction of hand motion during reaching movements in three-dimensional space ( 172 ) . Each neuron ii has a preferred direction of motion represented as a vector 𝒅i\mbox{\boldmath\(d\)}_{i} . The vectors of different neurons are added up with a weighting function proportional to the cells firing rate ( 172 ) . For the rapid movements of less than one second that we consider here, a single neuron is expected to emit at most a few spikes. Therefore a desired trajectory can be represented as a target spatio-temporal spike pattern; see Fig. 19.17 .

Model neurons in motor cortex receive spike input from neurons in sensory areas that represent, e.g., the vertical movement of the ball that is launched at the beginning of the serve, as well as the intention of the player. During practice sessions, the aim is to associate the spatio-temporal spike pattern in the input layer with the target spike pattern in the layer of motor cortex neurons while the only feedback is the success signal available at the end of the movement.

Fig. 19.17 shows that a two-layer network of spiking neurons can learn this task, if synaptic connections use a reward-modulated STDP rule (R-STDP) where the Hebbian term HH in Eq. ( 19.47 ) is the pair-based STDP rule defined in Eq. ( 19.10 ). It is important that the global neuromodulatory signal provided at the end of each trial, is not the raw reward, but success defined as ‘reward - expected’ reward as in Eq. ( 19.48 ). If a single task has to be learned, the expected reward can be estimated from the running average over past trials. However, if several trajectories (e.g., two different serves or two different scales) have to be learned in parallel, then the expected reward needs to be estimated separately for each trajectory ( 157 ) .

R-STDP rules have also been used for several other tasks, e.g., ( 238; 153 ) .

Fig. 19.17: Learning with R-STDP. A. The input consists of 350 spike trains with a temporal precision of 20ms. 50 unspecific neurons fired for both tasks, whereas half of the other neurons fired only for task A or task B. The output consists of 200 spiking model neurons. B. Output spike trains were convolved with a filter (top). The resulting continuous signal for neuron ii is interpreted as speed of movement in direction did_{i}, where different neurons code for different directions. The two target trajectories (bottom, dashed lines) correspond to two different target spatio-temporal spike train patterns. After a learning period of 10 000 trials, the network output generates a trajectory (full black lines) close to the target trajectories.

© Cambridge University Press. This book is in copyright. No reproduction of any part of it may take place without the written permission of Cambridge University Press.