8 Noisy Input Models: Barrage of Spike Arrivals 8.1 Noise input 8.3 Subthreshold vs. Superthreshold regime

8.2 Stochastic spike arrival

A typical neuron, e.g., a pyramidal cell in the vertebrate cortex, receives input spikes from thousands of other neurons, which in turn receive input from their presynaptic neurons and so forth; see Fig. 8.4. While it is not impossible to incorporate millions of integrate-and-fire neurons into a huge network model, it is often reasonable to focus the modeling efforts on a specific subset of neurons, e.g., a column in the visual cortex, and describe input from other parts of the brain as a stochastic background activity.

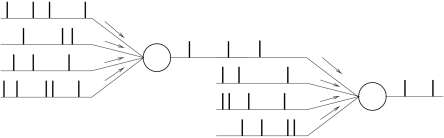
Fig. 8.4: Each neuron receives input spikes from a large number of presynaptic neurons. Only a small portion of the input comes from neurons within the model network; other input is described as stochastic spike arrival.

Let us consider a nonlinear integrate-and-fire neuron with index $i$ that is part of a large network. Its input consists of (i) an external input $I_{i}^{\rm ext}(t)$ ; (ii) input spikes $t_{j}^{(f)}$ from other neurons $j$ of the network; and (iii) stochastic spike arrival $t_{k}^{(f)}$ due to the background activity in other parts of the brain. The membrane potential $u_{i}$ evolves according to

\frac{{\text{d}}}{{\text{d}}t}u_{i}={f(u_{i})\over\tau_{m}}+{1\over C}I^{\rm ext% }(t)+\sum_{j}\sum_{t_{j}^{(f)}}w_{ij}\,\delta(t-t_{j}^{(f)})\,+\sum_{k}\sum_{t% _{k}^{(f)}}w_{ik}\,\delta(t-t_{k}^{(f)})\,,

(8.19)

where $\delta$ is the Dirac $\delta$ function and $w_{ij}$ is the coupling strength from a presynaptic neurons $j$ in the network to neuron $i$ . Input from background neurons is weighted by the factor $w_{ik}$ . While the firing times $t_{j}^{(f)}$ are generated by the threshold crossings of presynaptic integrate-and-fire neurons, the firing times $t_{k}^{(f)}$ of a background neuron $k$ are generated by a Poisson process with mean rate $\nu_{k}$ .

To simplify the following discussions we adopt three simplifications. First, we focus on a leaky integrate-and-fire neuron and shift the voltage so that the resting potential is at zero. Hence we can set $f(u)=-u$ . Second, we concentrate on a single neuron receiving stochastic input from background neurons. Hence we can drop the sum over $j$ which represents input from the network and also drop the index $i$ of our specific neuron. We therefore arrive at

\frac{{\text{d}}}{{\text{d}}t}u=-{u\over\tau_{m}}+{1\over C}I^{\rm ext}(t)+% \sum_{k}\sum_{t_{k}^{(f)}}w_{k}\,\delta(t-t_{k}^{(f)})\,,

(8.20)

The membrane potential is reset to $u_{r}$ whenever it reaches the threshold $\vartheta$ . Eq. (8.20) is called Stein’s model (494; 495).

In Stein’s model, each input spike generates a postsynaptic potential $\Delta u(t)=w_{k}\epsilon(t-t_{k}^{(f)})$ with $\epsilon(s)=e^{-s/\tau_{m}}\,\Theta(s)$ , i.e., the potential jumps upon spike arrival by an amount $w_{k}$ and decays exponentially thereafter. Integration of Eq. (8.20) yields

u(t|\hat{t})=u_{r}\,\exp(-{t-\hat{t}\over\tau_{m}})+{1\over C}\int_{0}^{t-\hat% {t}}\exp(-{s\over\tau_{m}})\,I(t-s)\,{\text{d}}s+\sum_{k=1}^{N}\sum_{t_{k}^{(f% )}}w_{k}\epsilon(t-t_{k}^{(f)})

(8.21)

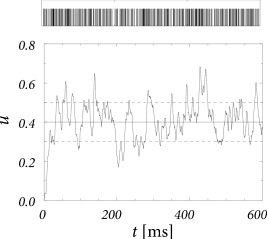
for $t>\hat{t}$ where $\hat{t}$ is the last firing time of the neuron. It is straightforward to generalize the model so as to include a synaptic time constant and work with arbitrary postsynaptic potentials $\epsilon(s)$ that are generated by stochastic spike arrival; cf. Fig. 8.5A.

8.2.1 Membrane potential fluctuations caused by spike arrivals

In order to calculate the fluctuations of the membrane potential caused by stochastic spike arrival, we assume that the firing threshold is relatively high and the input weak so that the neuron does not reach its firing threshold. Hence, we can safely neglect both threshold and reset. The leaky integrate-and-fire model of Stein (Eq. (8.21)) is then equivalent to a model of a passive membrane driven by stochastic spike arrival.

We assume that each input spike evokes a postsynaptic potential $w_{0}\,\epsilon(s)$ of the same amplitude and shape, independent of $k$ . The input statistics is assumed to be Poisson, i.e., firing times are independent. Thus, the total input spike train (summed across all synapses)

S(t)=\sum_{k=1}^{N}\sum_{t_{k}^{(f)}}\delta(t-t_{k}^{(f)})\,,

(8.22)

that arrives at neuron $i$ is a random process with expectation

\langle S(t)\rangle=\nu_{0}

(8.23)

and autocorrelation

\langle S(t)\,S(t^{\prime})\rangle-\,\nu_{0}^{2}=\nu_{0}\,\delta(t-t^{\prime})\,;

(8.24)

cf. Eq. (7.46).

Fig. 8.5: Input spikes arrive stochastically (upper panel) at a mean rate of 1 kHz. A. Each input spike evokes an excitatory postsynaptic potential (EPSP) $\epsilon(s)\propto s\exp(-s/\tau)$ with $\tau=4\,$ ms. The first EPSP (the one generated by the spike at $t=0$ ) is plotted. The EPSPs of all spikes sum up and result in a fluctuating membrane potential $u(t)$ . B. Continuation of the simulation shown in A. The horizontal lines indicate the mean (dotted line) and the standard deviation (dashed lines) of the membrane potential.

Suppose that we start the integration of the passive membrane equation at $t=-\infty$ with initial condition $u_{r}=0$ . We rewrite Eq. (8.21) using the definition of the spike train in Eq. (8.22)

u(t)={1\over C}\int_{0}^{\infty}\exp(-{s\over\tau_{m}})\,I(t-s)\,{\text{d}}s+w% _{0}\int_{0}^{\infty}\epsilon(s)\,S(t-s)\,{\text{d}}s\,.

(8.25)

Obviously, the integration over the $\delta$ -function in the last term on the right-hand side is possible and would lead back to the more compact representation $w_{0}\sum_{t_{k}^{(f)}}\epsilon(t-t_{k}^{(f)})$ . The advantage of having the spike train $S(t)$ appear explicitly is that we can exploit the definition of the random process $S$ , in particular, its mean and variance.

We are interested in the mean potential $u_{0}(t)=\langle u(t)\rangle$ and the variance $\langle\Delta u^{2}\rangle=\langle[u(t)-u_{0}(t)]^{2}\rangle$ . Using Eqs. (8.23) and (8.24) we find

u_{0}(t)={1\over C}\int_{0}^{\infty}\exp(-{s\over\tau_{m}})\,I(t-s)\,{\text{d}% }s+w_{0}\,\nu_{0}\,\int_{0}^{\infty}\epsilon(s)\,{\text{d}}s

(8.26)

and

	$\displaystyle\langle\Delta u^{2}\rangle$	$\displaystyle=w_{0}^{2}\,\int_{0}^{\infty}\int_{0}^{\infty}\epsilon_{0}(s)\,% \epsilon_{0}(s^{\prime})\,\,\langle S(t)\,S(t^{\prime})\rangle\,{\text{d}}s\,{% \text{d}}s^{\prime}\,-u_{0}^{2}$
		$\displaystyle=w_{0}^{2}\,\nu_{0}\int_{0}^{\infty}\epsilon^{2}(s)\,{\text{d}}s\,.$		(8.27)

In Fig. 8.5 we have simulated a neuron which receives input from $N=100$ background neurons with rate $\nu_{0}=10\,$ Hz. The total spike arrival rate is therefore $\nu_{0}=$ 1 kHz. Each spike evokes an EPSP $w_{0}\,\epsilon(s)=0.1\,(s/\tau)\,\exp(-s/\tau)$ with $\tau=4$ ms. The evaluation of Eqs. (8.26) and (8.2.1) for constant input $I=0$ yields $u_{0}=0.4$ and $\sqrt{\langle\Delta u^{2}\rangle}=0.1$ .

Example: Stein’s model with step current input

In Stein’s model each background spike evokes an EPSP $\epsilon(s)=e^{-s/\tau_{m}}$ . In addition, we assume a step current input which switches at $t=0$ from zero to $I_{0}$ ( $I_{0}<0$ ).

Mean and fluctuations for Stein’s model can be derived by evaluation of Eqs. (8.26) and (8.2.1) with $\epsilon(s)=e^{-s/\tau_{m}}$ . The result is

	$\displaystyle u_{0}$	$\displaystyle=$	$\displaystyle I_{0}\,[1-\exp(-{t/\tau_{m}})]+w_{0}\,\nu_{0}\,\tau_{m}$		(8.28)
	$\displaystyle\langle\Delta u^{2}\rangle$	$\displaystyle=$	$\displaystyle 0.5\,w_{0}^{2}\,\nu_{0}\,{\tau_{m}}$		(8.29)

Note that with stochastic spike arrival at excitatory synapses, as considered here, mean and variance cannot be changed independently. As we will see in the next subsection, a combination of excitation and inhibition allows us to increase the variance while keeping the mean of the potential fixed.

8.2.2 Balanced excitation and inhibition

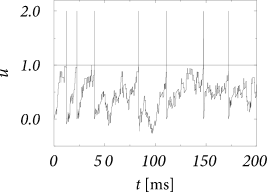
Let us suppose that an integrate-and-fire neuron defined by Eq. (8.20) with $\tau_{m}=10$ ms receives input from 100 excitatory neurons ( $w_{k}=+0.1$ ) and 100 inhibitory neurons ( $w_{k}=-0.1$ ). Each background neuron $k$ fires at a rate of $\nu_{k}$ = 10 Hz. Thus, in each millisecond, the neuron receives on average one excitatory and one inhibitory input spike. Each spike leads to a jump of the membrane potential of $\pm 0.1$ . The trajectory of the membrane potential is therefore similar to that of a random walk subject to a return force caused by the leak term that drives the membrane potential always back to zero; cf. Fig. 8.6A.

If, in addition, a constant stimulus $I^{\rm ext}=I_{0}>0$ is applied so that the mean membrane potential (in the absence of the background spikes) is just below threshold, then the presence of random background spikes may drive $u$ toward the firing threshold. Whenever $u\geq\vartheta$ , the membrane potential is reset to $u_{r}=0$ .

Since firing is driven by the fluctuations of the membrane potential, the interspike intervals vary considerably; cf. Fig. 8.6. Balanced excitatory and inhibitory spike input could thus contribute to the large variability of interspike intervals in cortical neurons; see Section 8.3.

Fig. 8.6: A. Voltage trajectory of an integrate-and-fire neuron ( $\tau_{m}=10\,$ ms, $u_{r}=0$ ) driven by stochastic excitatory and inhibitory spike input at $\nu_{+}=\nu_{-}=1$ kHz. Each input spike causes a jump of the membrane potential by $w_{\pm}=\pm 0.1$ . The neuron is biased by a constant current $I_{0}=0.8$ which drives the membrane potential to a value just below the threshold of $\vartheta=1$ (horizontal line). Spikes are marked by vertical lines. B. Similar plot as in A except that the jumps are smaller ( $w_{\pm}=\pm 0.025$ ) while rates are higher ( $\nu_{\pm}=16\,$ kHz).

With the above set of parameters, the mean of the stochastic background input vanishes since $\sum_{k}w_{k}\,\nu_{k}=0$ . Using the same arguments as in the previous example, we can convince ourselves that the stochastic arrival of background spikes generates fluctuations of the voltage with variance

\langle\Delta u^{2}\rangle=0.5\,\tau_{m}\sum_{k}w_{k}^{2}\,\nu_{k}=0.1\,;

(8.30)

cf. Section 8.4 for a different derivation.

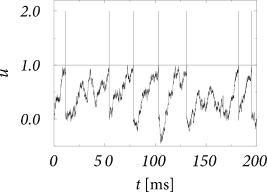
Let us now increase all rates by a factor of $a>1$ and multiply at the same time the synaptic efficacies by a factor $1/\sqrt{a}$ . Then both mean and variance of the stochastic background input are the same as before, but the size $w_{k}$ of the jumps is decreased; cf. Fig. 8.6B. In the limit of $a\to\infty$ the jump process turns into a diffusion process and we arrive at the stochastic model of Eq. (8.7). In other words, the balanced action of the excitatory and inhibitory spike trains, $S^{\rm exc}$ and $S^{\rm inh}$ respectively, arriving at the synapses with Poisson input rate $<S^{\rm exc}>=<S^{\rm inh}>=a\,\nu$ yields in the limit $a\to\infty$ a white noise input

{w\over\sqrt{a}}S^{\rm exc}-{w\over\sqrt{a}}S^{\rm inh}.\longrightarrow\xi(t)

(8.31)

The above transition is called the diffusion limit and will be systematically discussed in Section 8.4. Intuitively, the limit process implies that in each short time interval $\Delta t$ a large number of excitatory and inhibitory input spikes arrive, each one causing the membrane potential to jump by a tiny amount upward or downward.

Example: Synaptic time constants and colored noise

In contrast to the previous discussion of balanced input, we now assume that each spike arrival generated a current pulse $\alpha(s)$ of finite duration so that the total synaptic input current is

R\,I(t)=w^{\rm exc}\int_{0}^{\infty}\alpha(s)\,S^{\rm exc}(t-s){\text{d}}s-w^{% \rm inh}\int_{0}^{\infty}\alpha(s)\,S^{\rm inh}(t-s){\text{d}}s.

(8.32)

If the spike arrival is Poisson with rates $<S^{\rm exc}>=<S^{\rm inh}>=a\,\nu$ and the synaptic weights are $w^{\rm exc}=w^{\rm inh}=w/\sqrt{a}$ , then we can take the limit $a\to\infty$ with no change of mean or variance. The result is colored noised.

An instructive case is $\alpha(s)=(1/\tau_{s})\exp(-s/\tau_{s})\Theta(s)$ with synaptic time constant $\tau_{s}$ . In the limit $\tau_{s}\to 0$ we are back to white noise.