13 Continuity Equation and the Fokker-Planck Approach 13.2 Stochastic spike arrival 13.4 Networks of leaky integrate-and-fire neurons

13.3 Fokker-Planck equation

The equation for the membrane potential density in a population of integrate-and-fire neurons (see Eq. (13.14) in the previous section) can, in the limit of small jump amplitudes $w_{k}$ , be approximated by a diffusion equation. To show this, we expand the right-hand side of Eq. (13.14) into a Taylor series up to second order in $w_{k}$ . The result is the Fokker-Planck equation,

$\displaystyle\tau_{m}{\partial\over\partial t}p(u,t)$	$\displaystyle=$	$\displaystyle-{\partial\over\partial u}\left\{\left[f(u)+R\,I^{\rm ext}(t)+% \tau_{m}\sum_{k}\nu_{k}(t)\,w_{k}\right]\,p(u,t)\right\}$	(13.16)
		$\displaystyle+{1\over 2}\,\left[\tau_{m}\sum_{k}\nu_{k}(t)\,w_{k}^{2}\right]\,% {\partial^{2}\over\partial u^{2}}p(u,t)$
		$\displaystyle+\tau_{m}\,A(t)\,\delta(u-u_{r})-\tau_{m}\,A(t)\,\delta(u-\theta_% {\rm reset})+{\mathcal{O}}(\omega_{k}^{3})\,.$

The term with the second derivative describes a ‘diffusion’ in terms of the membrane potential.

It is convenient to define the total ‘drive’ in voltage units as

\mu(t)=R\,I^{\rm ext}(t)+\tau_{m}\sum_{k}\nu_{k}(t)\,w_{k}

(13.17)

and the amount of diffusive noise (again in voltage units) as

\sigma^{2}(t)=\tau_{m}\sum_{k}\nu_{k}(t)\,w_{k}^{2}\,.

(13.18)

The firing threshold acts as an absorbing boundary so that the density at threshold vanishes:

p(\theta_{\rm reset},t)=0\,.

(13.19)

The boundary condition $p(\theta_{\rm reset},t)=0$ arises from the mathematical limiting process: We consider that all weights go to zero, $w_{k}\to 0$ , while the total drive $\mu$ and the amount of diffusive noise remains constant. This is only possible if we have at least two different types of synapse (excitatory and inhibitory) and we increase the rate of both while decreasing the weights of synapses. In other words, the spike arrival rates at the synapses go to infinity so that the ‘shot noise’ generated by spike arrivals turns into a white Gaussian distributed noise. Any neuron with a membrane potential just below threshold would then immediately fire because of the noise. Therefore the density at threshold has to be zero. This argument is no longer valid, if spike arrival rates are finite, or if synapses react slowly so that the noise is colored (cf. Section 13.6.4 below).

In order to calculate the flux through the reset threshold we expand Eq. (13.13) in $w_{k}$ about $u=\theta_{\rm reset}$ and obtain

A(t)=-\left.{\sigma^{2}(t)\over 2\tau_{m}}\,{\partial p(u,t)\over\partial u}% \right|_{u=\theta_{\rm reset}}\,,

(13.20)

Eqs. (13.16) – (13.20) together with the normalization (13.3) define the dynamics of a homogeneous population of integrate-and-fire neurons with ‘diffusive’ noise. For a more detailed discussion of the diffusion limit see Chapter 8, in particular Eqs. (8.41) and (8.43).

Example: Flux in the diffusion limit

If we compare the continuity equation (13.7) with the explicit form of the Fokker-Planck equation (13.16), we can identify the flux caused by stochastic spike arrival and external current in the diffusion limit

\,J^{\rm diff}(u,t)={f(u)+\mu(t)\over\tau_{m}}\,p(u,t)-{1\over 2}\,{\sigma^{2}% (t)\over\tau_{m}}{\partial\over\partial u}p(u,t).

(13.21)

We emphasize that stochastic spike arrival contributes to the mean drive $\mu(t)=R\,I^{\rm ext}(t)+\tau_{m}\sum_{k}\nu_{k}(t)\,w_{k}$ as well as to the diffusive noise $\sigma^{2}(t)=\tau_{m}\sum_{k}\nu_{k}(t)\,w_{k}^{2}$ .

13.3.1 Stationary solution for leaky integrate-and-fire neurons(*)

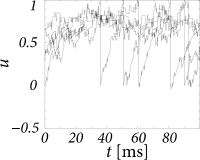
The stationary distribution $p(u)$ of the membrane potential is of particular interest, since it is experimentally accessible (86; 126; 108). We now derive the stationary solution $p(u,t)\equiv p(u)$ of the Fokker-Planck equation (13.16) for a population of leaky integrate-and-fire neurons. Neurons are described by Eq. (13.1) with $f(u)=-u$ , i.e., the voltage scale is shifted so that the equilibrium potential is at zero. For leaky integrate-and-fire neurons, the reset threshold is the same as the rheobase firing threshold and will be denoted by $\vartheta=\theta_{\rm reset}=\vartheta_{rh}$ .

We assume that the total input $h_{0}=R\,I^{\rm ext}+\tau_{m}\sum_{k}\nu_{k}\,w_{k}$ is constant. In the stationary state, the temporal derivative on the left-hand-side of Eq. (13.16) vanishes. The terms on the right-hand side can be transformed such that the stationary Fokker-Planck equation reads (for $u<\vartheta$ )

0=-{\partial\over\partial u}J(u)+A_{0}\,\delta(u-u_{r})\,,

(13.22)

where $A_{0}$ is the population activity (or mean firing rate) in the stationary state and

J(u)={-u+h_{0}\over\tau_{m}}\,p(u)-{1\over 2}{\sigma^{2}\over\tau_{m}}{% \partial\over\partial u}p(u)

(13.23)

is the total flux; cf. Eq. (13.6). The meaning of Eq. (13.22) is that the flux is constant except at $u=u_{r}$ where it jumps by an amount $A_{0}$ . Similarly, the boundary condition $p(\vartheta,t)=0$ implies a second discontinuity of the flux at $u=\vartheta$ .

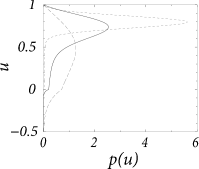
With the results from Chapter 8 in mind, we expect that the stationary solution approaches a Gaussian distribution for $u\to-\infty$ . In fact, we can check easily that for any constant $c_{1}$

p(u)={c_{1}\over\sigma}\exp\left[-{(u-h_{0})^{2}\over\sigma^{2}}\right]\quad{% \rm~{}for~{}}u\leq u_{r}

(13.24)

is a solution of Eq. (13.22) with flux $J(u)=0$ . However, for $u>u_{r}$ a simple Gaussian distribution cannot be a solution since it does not respect the boundary condition $p(\vartheta)=0$ . Nevertheless, we can make an educated guess and try a modified Gaussian, (188; 78)

p(u)={c_{2}\over\sigma^{2}}\exp\left[-{(u-h_{0})^{2}\over\sigma^{2}}\right]\,% \cdot\,\int_{u}^{\vartheta}\exp\left[{(x-h_{0})^{2}\over\sigma^{2}}\right]\,{% \text{d}}x\quad{\rm~{}for~{}}u_{r}<u\leq\vartheta\,,

(13.25)

with some constant $c_{2}$ . We have written the above expression as a product of two terms. The first factor on the right-hand side is a standard Gaussian while the second factor guarantees that $p(u)\to 0$ for $u\to\vartheta$ . If we insert Eq. (13.25) in (13.22) we can check that it is indeed a solution. The constant $c_{2}$ is proportional to the flux,

c_{2}=2\,\tau_{m}\,J(u)\quad{\rm~{}for~{}}u_{r}<u\leq\vartheta\,.

(13.26)

The solution defined by Eqs. (13.24) and (13.25) must be continuous at $u=u_{r}$ . Hence

c_{1}={c_{2}\over\sigma}\int_{u_{r}}^{\vartheta}\exp\left[{(x-h_{0})^{2}\over% \sigma^{2}}\right]\,{\text{d}}x\,.

(13.27)

Finally, the constant $c_{2}$ is determined by the normalization condition (13.3). We use Eqs. (13.24), (13.25), and (13.27) in (13.3) and find

{1\over c_{2}}=\int_{-\infty}^{u_{r}}\int_{u_{r}}^{\vartheta}f(x,u)\,{\text{d}% }x\,{\text{d}}u+\int_{u_{r}}^{\vartheta}\int_{u}^{\vartheta}f(x,u)\,{\text{d}}% x\,{\text{d}}u=\int_{u_{r}}^{\vartheta}\int_{-\infty}^{x}f(x,u)\,{\text{d}}u\,% {\text{d}}x\,,

(13.28)

with

f(x,u)={1\over\sigma^{2}}\exp\left[-{(u-h_{0})^{2}\over\sigma^{2}}\right]\,% \exp\left[{(x-h_{0})^{2}\over\sigma^{2}}\right]\,.

(13.29)

Figure 13.5B shows the resulting stationary density $p(u)$ for different noise amplitudes.

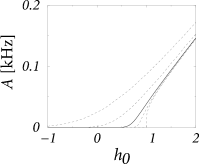
The activity $A_{0}$ is identical to the flux $J(u)$ between $u_{r}$ and $\vartheta$ and therefore proportional to the constant $c_{2}$ ; cf. Eq. (13.26). If we express the integral over $u$ in Eq. (13.28) in terms of the error function, ${\rm erf}(x)={2\over\sqrt{\pi}}\int_{0}^{x}\exp(-u^{2})\,{\text{d}}u$ , we obtain

A_{0}^{-1}=\tau_{m}\,\sqrt{\pi}\,\int_{{u_{r}-h_{0}\over\sigma}}^{{\vartheta-h% _{0}\over\sigma}}\,\exp\left({x}^{2}\right)\,\left[1+{\rm erf}(x)\right]\,{% \text{d}}x\,,

(13.30)

which is identical to the Siegert formula (476) of the single neuron firing rate [cf. Eqs. (8.54) or (12.26)] that we used previously in Chapters 8 and 12. An alternative formulation (see Exercises) of the remaining integral in Eq. (13.30) is also possible (78).