4 Dimensionality Reduction and Phase Plane Analysis 4 Dimensionality Reduction and Phase Plane Analysis 4.2 Reduction to two dimensions

4.1 Threshold effects

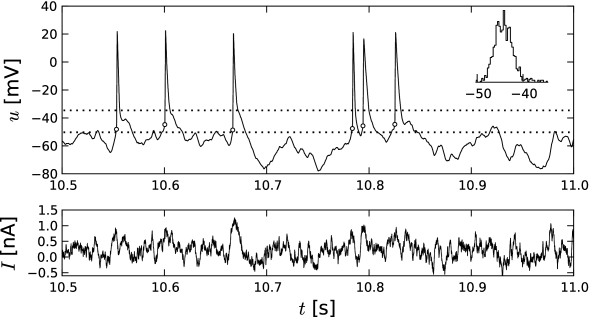
Many introductory textbooks of neuroscience state that neurons fire an action potential if the membrane potential reaches a threshold. Since the onset of an action potential is characterized by a rapid rise of the voltage trace, the onset points can be detected in experiment recordings (Fig. 4.1A). Intuitively, the onset of an action potential occurs when the membrane potential crosses the firing threshold.

The firing threshold is not only a useful concept for experimental neuroscience, it is also at the heart of most integrate-and-fire models and therefore central for Parts II and III of this book. But does a firing threshold really exist?

Experimentalists inject currents into a single neuron to probe its firing characteristics. There is a large choice of potential current wave forms, but only few of these are routinely used in many labs. In this section we use current pulses and steps in order to explore the threshold behavior of the Hodgkin-Huxley model.

Fig. 4.1: Firing threshold. A. Experimental recording of membrane voltage (top) during stimulation with a time-dependent current (bottom). The onset of spikes, defined as the moment when the voltage starts its upswing, is marked by open circles. The lowest and highest onset voltage during a recording of 20s are marked by dotted horizontal lines. Inset: Histogram of onset voltages; adapted from (340). B. Stimulation of the Hodgkin-Huxley model with pulse and step current. Voltage (top) in response to pulses and steps (bottom). The apparent voltage threshold is higher (dotted lines in top panel) for a pulse than for a step current. The critical currents are 16.6 $\mu$ A/cm ${}^{2}$ for the 1 ms pulse and 3.31 $\mu$ A/cm ${}^{2}$ for the step. Parameters of the Hodgkin-Huxley model as in Table 2.1.

4.1.1 Pulse Input

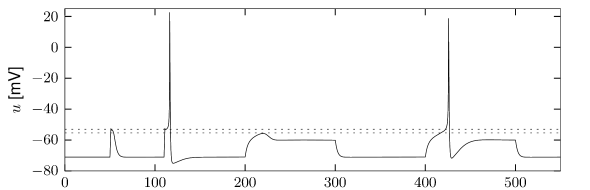
A Hodgkin-Huxley model is stimulated by a short current pulse of 1 ms duration. If the stimulus is strong enough, it elicits a spike. In Fig. 4.1AB the amplitude of the stimulating current is only slightly increased between the first and second current pulse. The membrane potential returns directly to the resting potential after the stimulus, while the neuron fires a spike in response to the second pulse. This seems to suggest that the voltage threshold for spike firing is just above the maximum voltage that is reached after the first current injection (upper horizontal dashed line in Fig. 4.1B.

Unfortunately, however, such an interpretation is incorrect. If we use a longer current pulse of 100 ms duration and apply the same argument as before, we would find a different voltage threshold, indicated by the lower horizontal dashed line in Fig. 4.1B.

Despite the fact that neuronal action potential firing is often treated as a threshold-like behavior, such a threshold is not well-defined mathematically (438; 268). For practical purposes, however, the transition can be treated as a threshold effect. However, the threshold we find depends, however, on the stimulation protocol.

For a mathematical discussion of the threshold phenomenon, it is helpful to reduce the system of four differential equations to two equations; this is the topic of Section 4.2. We will return to pulse currents in Section 4.5.

Example: Short current pulse as voltage step

The above argument excludes a voltage threshold, but could there be a current threshold? Instead of injecting a current of 1ms duration we can use a shorter pulse that only lasts half as long. Numerically, we find that the minimal current necessary to trigger an action potential of the Hodgkin-Huxley model, is now twice as large as before. We conclude that, for short current pulses, it is not the amplitude of the current that sets the effective firing threshold, but rather the integral of the current pulse or the charge. Indeed, the more charge we put on the membrane the higher the voltage, simply because of the capacitance $C$ of the membrane. For very short current pulses

I(t)=q\,\delta(t)=\lim_{\Delta\to 0}{q\over\Delta}\quad{\rm for~{}}{0<t<\Delta% }\quad{\rm and~{}}0{\rm~{}otherwise}.

(4.1)

the voltage of the Hodgkin-Huxley model increases at the moment of current injection by an amount $\Delta u=q/C$ where $q$ is the charge of the current pulse (see Section 1.3.2 in Chapter 1). If the model was at rest for $t<0$ , the new voltage $u=u_{\rm rest}+\Delta u$ can be used as the initial condition for the numerical integration of the Hodgkin-Huxley model for times $t>0$ . Thus, a short current pulse amounts to a step-like increase of the voltage by a fixed amount.

4.1.2 Step Current Input

In Chapter 2 we have seen that a constant input current $I_{0}>I_{\theta}$ can generate regular firing. In this paragraph we study the response of the Hodgkin-Huxley model to a step current of the form

I(t)=I_{1}+\Delta I\,{\mathcal{H}}(t)\,.

(4.2)

Here ${\mathcal{H}}(t)$ denotes the Heaviside step function, i.e., ${\mathcal{H}}(t)=0$ for $t\leq 0$ and ${\mathcal{H}}(t)=1$ for $t>0$ . At $t=0$ the input jumps from a fixed value $I_{1}$ to a new value $I_{2}=I_{1}+\Delta I$ ; see Fig. 4.2A. We may wonder whether spiking for $t>0$ depends only on the final value $I_{2}$ or also on the step size $\Delta I$ .

The answer to this question is given by Fig. 4.2D. A large step $\Delta I$ facilitates the spike initiation. For example, a target value $I_{2}=2\mu$ A/cm ${}^{2}$ elicits a spike, provided that the step size is large enough, but does not cause a spike if the step is small. The letter $S$ in Fig. 4.2D denotes the regime where only a single spike is initiated. Repetitive firing (regime $R$ ) is possible for $I_{2}>2.6\mu$ A/cm ${}^{2}$ , but must be triggered by sufficiently large current steps.

Fig. 4.2: Phase diagram for stimulation with a step current. A. The input current $I(t)$ changes at $t=0$ from $I_{1}$ to $I_{2}$ . B,C,E. Sample responses of the Hodgkin-Huxley model to step current input. D The outcome of the simulation experiment as a function of the final current $I_{2}$ and the step size $\Delta I=I_{2}-I_{1}$ . Three regimes denoted by $S,R$ , and $Q$ may be distinguished. In $Q$ no action potential is initiated (quiet regime). In $S$ , a single spike is initiated by the current step (single spike regime). In $R$ , periodic spike trains are triggered by the current step (repetitive firing). Examples of voltage traces in the different regimes are presented in the smaller graphs (B,C,E) with stimulation parameters indicated by the filled circles in D. Note that for the same final current $I_{2}$ (e.g. 2.0 $\mu$ A/cm ${}^{2}$ ), the neuron model emits a spike if the current step $\Delta I$ is large enough (regime S), or no spike if the step is too small. For a final current $I_{2}=3$ $\mu$ A/cm ${}^{2}$ , the model exhibits bistability between repetitive firing and quiescence.

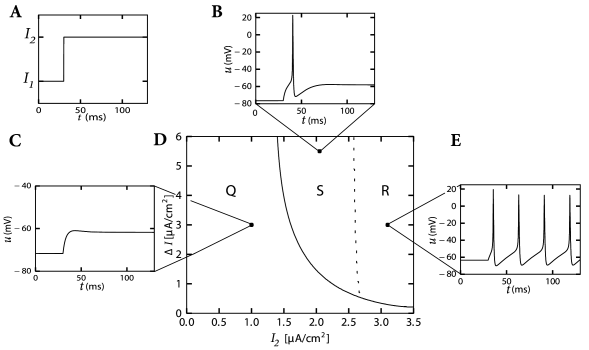
We may conclude from Fig. 4.2D that, when probing with step currents, there is neither a unique current threshold for spike initiation nor for repetitive firing. The trigger mechanism for action potentials depends not only on $I_{2}$ but also on the size of the current step $\Delta I$ .

Biologically, the dependence upon the step size arises from the different time constants of activation and inactivation of the ion channels. Mathematically, the stimulation with step currents can be analyzed transparently in two dimensions (Sections 4.3 and 4.4).